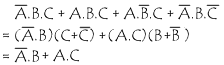Loi de composition

Les lois de composition

Les lois de composition sont des règles logiques qui permettent de simplifier l'écriture des expressions algébriques.

Associativité

  • (A.B).C est équivalent à A.(B.C)
  • (A+B)+C est équivalent à A+(B+C)

Absorption

  • A.(A+B) est équivalent à A
  • A+A.B est équivalent à A

Commutativité

  • A.B est équivalent à B.A
  • A+B est équivalent à B+A

Distributivité

  • A+(B.C) est équivalent à (A+B).(A+C)
  • A.(B+C) est équivalent à A.B+A.C

Idempotence

  • A.A est équivalent à A
  • A + A est équivalent à A

Identité

  • 1.A est équivalent à A
  • 0+A est équivalent à A

Inversion

  • A./A est équivalent à 0
  • A+/A est équivalent à 1

Nullité

  • 0.A est équivalent à 0
  • 1+A est équivalent à 1

Théorème de De Morgan

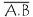  • est équivalent à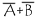
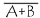  • est équivalent à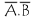

Remarque d'un visiteur

A titre informatif, il est possible de prouver la loi d'absorption avec les autres lois : 


A.(A+B)
= A.A + A.B
= A + A.B
= A.1 + A.B
= A.(1+B)
= A
Sur la deuxième ligne, la deuxième loi d'absorption apparaît.

Exemple de simplification d'expression

Soit la simplification suivante :

Réalisé sous la direction de , fondateur de CommentCaMarche.net.

Ce document intitulé «  Loi de composition  » issu de CommentCaMarche (www.commentcamarche.net) est mis à disposition sous les termes de la licence Creative Commons. Vous pouvez copier, modifier des copies de cette page, dans les conditions fixées par la licence, tant que cette note apparaît clairement.